Back To The Basics

I’ve decided to compile the notes I’ve made over the course of my ML journey as a series of blog posts here on my website. I’ve revised machine learning, deep learning and natural language processing concepts a couple of times since beginning my ML journey almost 3 years ago, and found that each time I revised, I added a deeper level of understanding about these concepts.

Machine learning is not an easy field to begin with, and the constant evolution of the field can lead ML practitioners to feel overwhelmed and outdated. That’s why I recommend periodically refreshing your knowledge and setting up “living” notes that you can add to each time you learn or revise.

You can view other topics in this series by clicking on the ML NOTES category in the article header above.

Disclaimer

I’ve read through multiple sources; articles, documentation pages, research papers and textbooks, to compile my notes. I was looking to maximise my understanding of the concepts and, previously, never intended to share them with the world. So, I did not do a good job of documenting sources for reference later on.

I’ll leave references to source materials if I have them saved. Please note that I’m not claiming sole authorship of these blog posts; these are just my personal notes and I’m sharing them here in the hopes that they’ll be helpful to you in your own ML journey.

Take these articles as a starting point to comprehend the concepts; there might be mistakes or errors in these articles. If you spot any or have other suggestions for improvement, please feel free to reach out to me & share your thoughts through my LinkedIn.

We’ll start with understanding errors in machine learning models, particularly bias and variance.

Errors in Machine Learning models

The goal of training a machine learning model (via supervised learning) is to create a model that is able to perform well (how well? criteria usually laid down by domain experts along with ML teams) on new data when this model is used in the real world.

Now, no model is capable of perfect predictions every time as each model will always have some amount of error baked in to it.

This error can be divided into 2 components; irreducible error and reducible error. As the name suggests irreducible error is something that cannot be reduced, due to a number of reasons, including:

Underlying data used to train the model; more diverse and expansive the dataset the better, but in the real world finding datasets that are comprehensive enough to cover all possible outcomes of an event including all possible factors is a very difficult and rare occurence.
Assumptions the model makes about the dataset. Each model has some built-in assumptions about the form of the target function which maps the inputs to the outputs. This is done to make the “learning” task easier at the liberty of (some amount of) accuracy.
Lack of computational resources + time; most businesses do not have infinite budgets to extensively train models for long durations on large datasets.
Imperfect datasets; most businesses have to deal with a lot of errors/inconsistencies in their dataset that requires a lot of manual effort to correct.

Reducible error

The reducible error component however can be reduced through various techniques which may result in improving the model’s accuracy.

Reducible error of a model includes bias and variance.

Bias

Bias is defined as the difference between the model’s predicted values and the ground truth values. Bias occurs due to the assumptions an algorithm makes regarding the target function to make learning the target function a simpler task.

A target function maps the input to the outputs, and most ML models attempt to (approximately) re-create the form of this function to produce predictions.

Models can be either low-bias or high-bias:

Low bias models make fewer assumptions about the target functions, so these models are able to learn non-linear or complex relationships in the data better. A few examples include neural networks, decision trees etc.
High bias models make more assumptions about the target function to make the learning task (learning to approximate the form of the target function) simpler. As a result, high bias models are unable to capture complex or non-linear relationships between the features and are best suited to tasks where the data shows a linear relationship. Generally, “simple” models such as linear regression, logistic regression etc, are said to have high bias.

Therefore, you need to carefully analyse your data to probe its characteristics before moving on to the modelling phase. Fitting a high-bias model on non-linear data may result in poor predictive performance as there is a mismatch between the model’s assumption about the form of the target function needed to map the inputs to the outputs, and, the underlying characteristics of the data.

Variance

Variance is described as the difference in the performance of the model when the training dataset is changed. Ideally, a good model should capture the characteristics of the data well enough that it is able to produce consistent predictions when a slightly different training dataset is used.

Low variance models are those whose predictions do not vary much when the training dataset is changed. Examples of low variance models include linear regression, logistic regression. Notice that these are high-bias models.
High variance models are those whose predictions vary widely with different training datasets. A few high variance models include neural networks, SVM, etc. High variance models are more prone to overfitting; not able to generalise well on new samples.

Bias-Variance Tradeoff

Bias and variance in a model are inversely related and there is said to be a “tradeoff” between the 2 qualities; for example if you want to reduce the bias of a model, you might end up increasing its variance. So, an optimal tradeoff between the bias and variance has to be made to achieve a balance between the two.

The interplay of bias and variance can lead to 4 scenarios:

Low Bias + Low Variance

Figure 1: Predictions are consistent (v) and accurate (b). Ideal scenario.

Low Bias + High Variance

Figure 2: Predictions are accurate (b) but inconsistent (v). Case of overfitting

High Bias + Low Variance

Figure 3: Predictions are consistent (v) but inaccurate (b). Case of underfitting.

High Bias + High Variance

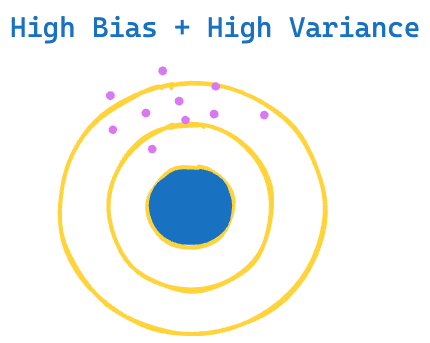
Figure 4: Predictions are inaccurate (b) and inconsistent (v). Trash model probably.

Having an understanding of bias and variance can help you choose models for your specific task and dataset. Hope you’ve found this post helpful, and as always, pop in occasionally in this space to read more on machine learning.